开发填充空间的分形

开发填充空间的分形

EasyRef
参数化

开发填充空间的分形

深入探索数学、分形、几何以及填充空间曲线的世界。

前言

继上一篇关于“…第一、第二和第三维度，以及为什么分形不属于其中任何一个…”的文章之后，本篇是我记录自己更深入探索分形、数学和几何的过程。

分形的研究是一个极其庞大的课题，甚至足以耗费数个生命去探索。尽管如此，我选择将焦点放在单曲线几何上。但请记住，我实际上只是在触碰这个领域的冰山一角。

 

4.0 经典空间填充

受到 19 世纪末格奥尔格·康托尔关于无限研究的启发，数学家们试图找到一种方法，把一维线映射到二维空间——一种能够穿过给定空间中每个点的曲线。

Jeffrey Ventrella 写道：“空间填充曲线可以被描述为一种从低维空间到高维空间的连续映射。” 换句话说，一条一维曲线通过增加其长度和曲率，被发展为在二维空间中占据更多面积。在数学世界中，曲线没有厚度，空间无限，因此这种过程可以无限进行。

 

4.1 早期示例

1890 年，朱塞佩·皮亚诺发现了第一个所谓的空间填充曲线：

皮亚诺曲线的 4 次迭代

起始画出一条“曲线”，然后用整个曲线替换其中的每个元素。如此重复四次，可以想象这个过程能够无限继续。人们会认为，当无限迭代后，这条一维曲线最终会填满整个二维空间并成为一个面。然而由于曲线没有厚度，它永远不会真正成为一个面，只是无限接近而已。（我想……我不太确定……）

一年后，大卫·希尔伯特提出了更简单的空间填充曲线。

希尔伯特曲线的 8 次迭代

1904 年，赫尔格·冯·科赫利用基础几何生成了一条复杂的连续曲线。

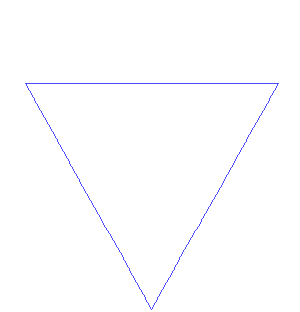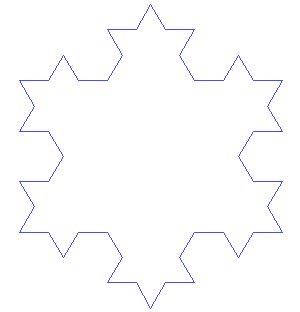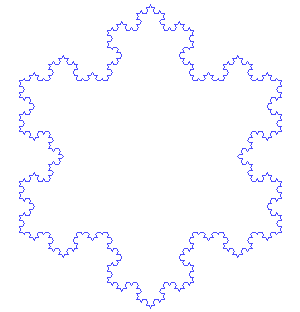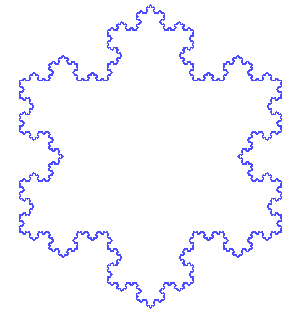
科赫曲线的 7 次迭代

1967 年左右，NASA 的物理学家 John Heighway、Bruce Banks 和 William Harter 发现了现在广为人知的“龙形曲线”。

龙形曲线的 13 次迭代

 

4.2 后期示例

妳可能注意到，有些曲线比其他曲线更能有效填充空间，这与它们的维数测度有关。它们被归类为分形，因为它们既不是一维的，也不是二维的，而是介于两者之间。曲线迭代无限次时，其分形维度决定了它们填充空间的程度。

这些是最早的空间填充曲线之一，但实际上可能存在无穷多的变体。Jeffrey Ventrella 用超过 25 年研究分形曲线，并在《Brain-Filling Curves, A Fractal Bestiary》一书中展示了 200 多种。他根据分形曲线的家族分类法组织，并为其赋予独特的遗传编码。

顺便一提，在我尝试复现 Ventrella 书中的某个分形时，不小心创造了一个略有不同的新分形。我把它暂时命名为“尼科利诺的四叶饰”。这个图形是我在 Rhino 和 Grasshopper 中结合 Anemone 创建的。

尼科利诺四叶形的 5 个版本

更多精美的空间填充曲线动画请见：

（以及“3Blue1Brown”制作的其他一些精彩视频，讨论了空间填充曲线、分形、无限数学等的性质）

 

奇特的一点

希尔伯特曲线的某个迭代版本（无限重复后）可以填充三维空间。

它是一条在空间中不断弯曲的一维曲线，通过简单重复的规则生成。逻辑上这可以无限进行，但这次结果不再是面，而是体积。换句话说，它从一维逐渐变为三维体积，却永远不会真正成为二维面。

这也支持了我在上一篇文章中的说法：“…根本不存在所谓的‘第一’或‘第二’维度，就像往花瓶里倒三杯水，再问别人哪一杯是第一杯，这个问题本身没有意义…”

 

5.0 前卫的空间填充

在最初的空间填充曲线中，目标是填充整个无限空间。但当我们改变生成规则时，其基本特性会发生剧烈变化。它们不必再如此数学化或几何纯粹。下面的曲线依然能无限细分，是真正的空间填充曲线，但特别之处在于我们可以控制填充的过程，而不是像原始曲线那样几乎没有艺术自由度。

 

5.1 旅行推销员问题

如果我们将规则改为：曲线只经过我们选择的点，那么问题就变成了著名的计算难题“旅行推销员问题”。

推销员希望在最短路径下访问所有城市，以最大化利润。但随着城市数量增加，可能的路径组合呈指数增长，问题极其复杂。

有多种不同的策略来解决这个问题，其中一些在这里有所介绍：

最终结果是一条单一的曲线，以一种独特而可控的方式填充空间。该方法可用于基于从 Voronoi 图中提取的点生成单线绘图，这是 Arjan Westerdiep 探索过的主题：

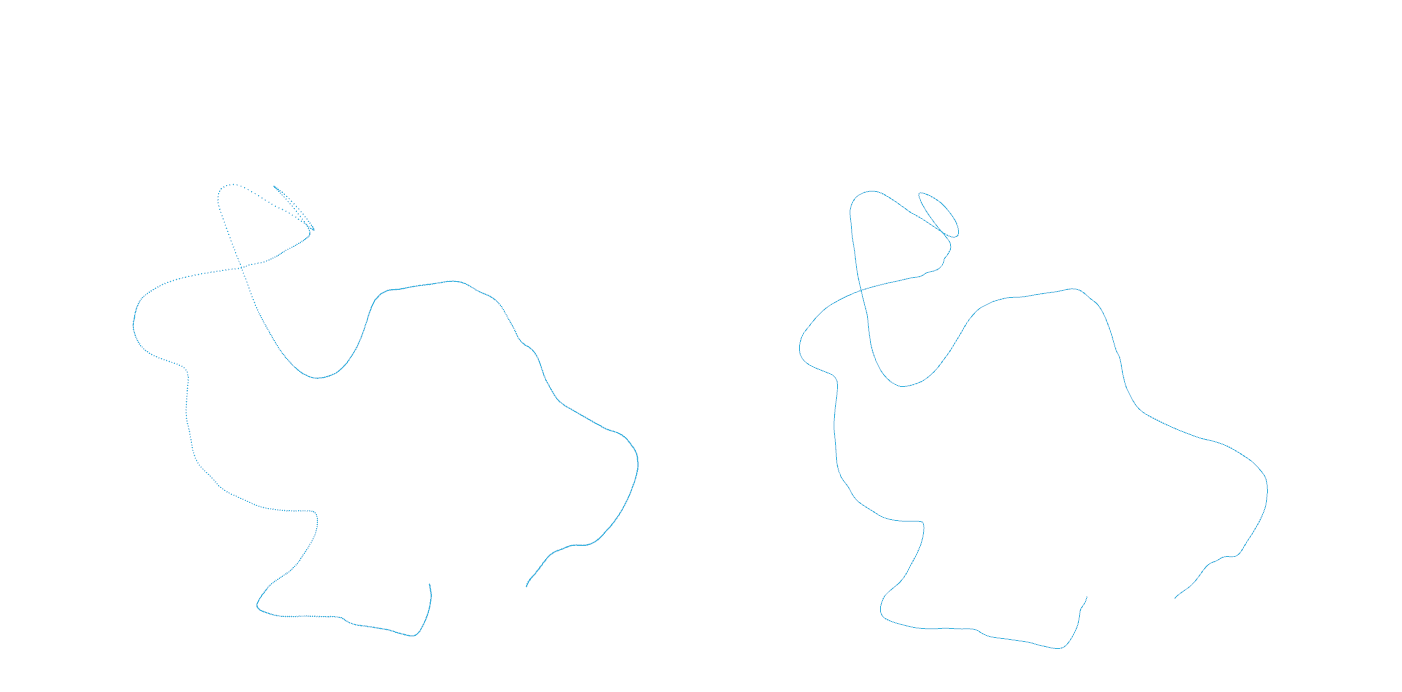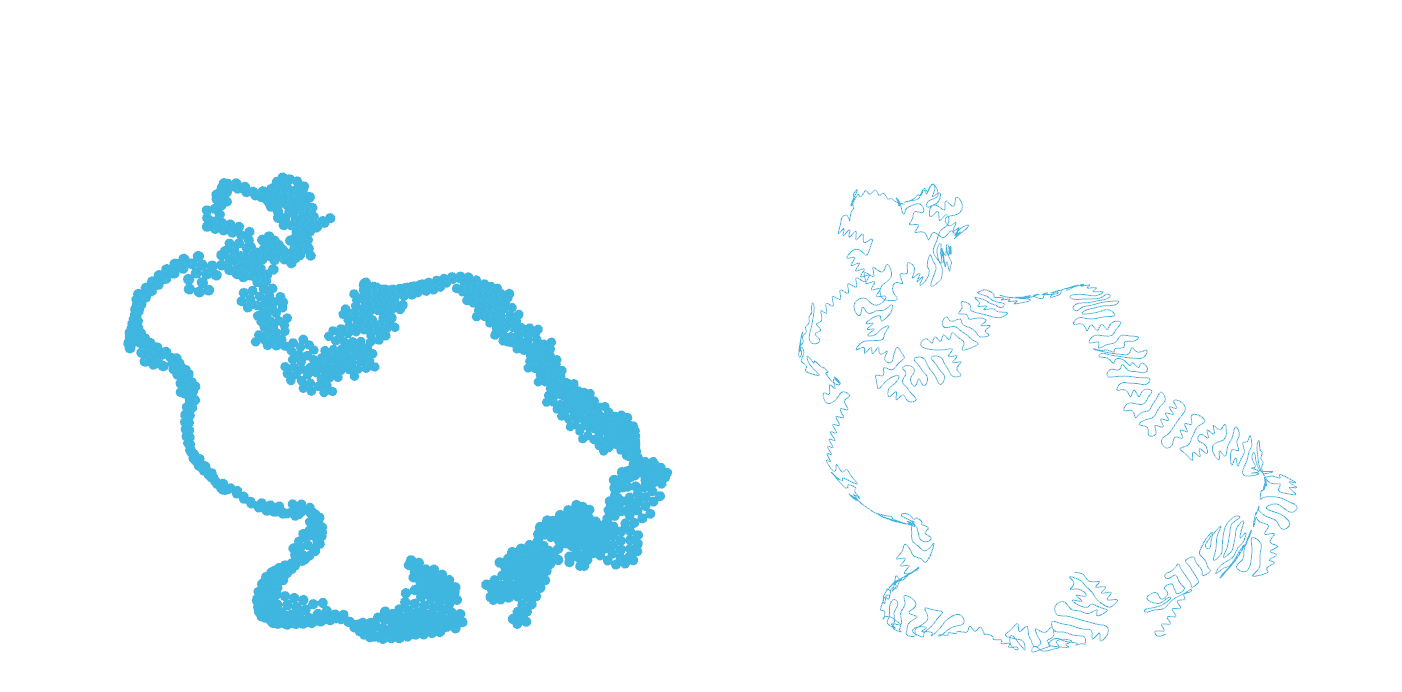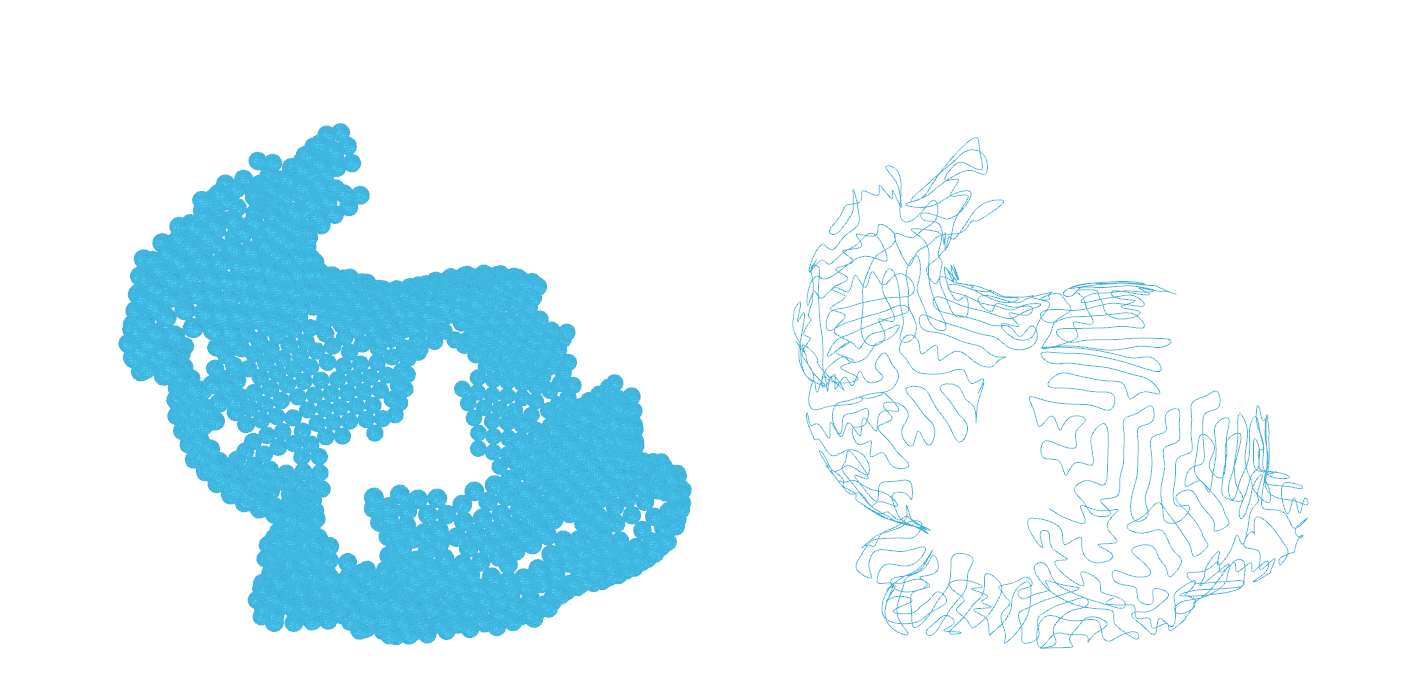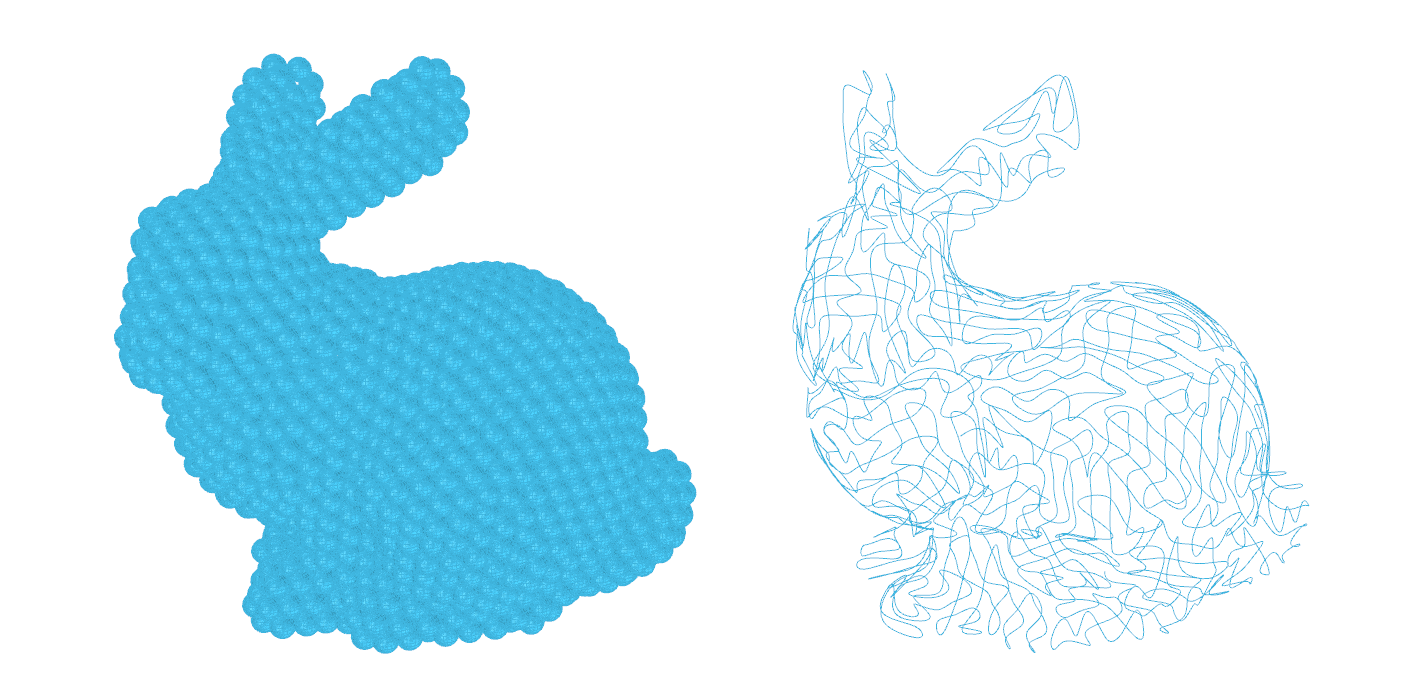
这幅插图由滑铁卢大学的比尔·库克委托创作，是旅行推销员问题的一个解决方案。

 

5.2 差分生长

如果我们让物理（而不是数学）决定曲线的生长，结果会变得更加有机且不那么受控。

在这个例子中，Rhino 搭配 Grasshopper 和 Kangaroo 2 被使用。一条曲线被绘制在平面上，分割成多个片段，然后逐渐延长。只要曲线不允许自我交叉（这里通过“碰撞球”实现），结果就是一条相当擅长均匀填充空间的曲线。

使用 Rhino 和 Grasshopper 实现差异化生长 – Kangaroo 2 – Planar

这种几何形态甚至不必局限于平面表面；它可以作用在任何二维表面（甚至三维，我猜测或者还可以是更高维度的空间）。

使用 Rhino 和 Grasshopper 实现差异生长 – Kangaroo 2 – NonPlanar

Rhino 和 Grasshopper 的差异生长 – Kangaroo 2 – 单曲线斯坦福兔

此外，Anemone 可以与 Kangaroo 2 配合使用，在曲线生长的同时不断进行细分。结果会更光滑，同时也更有机。

Rhino、Grasshopper 和 Kangaroo 2 与 Anemone 的差异生长——Octopus

当然，这个过程也可以反向进行，使曲线能够无缝地从一个空间流动到另一个空间。

Rhino 和 Grasshopper 的差异化生长 – Kangaroo 2 和 Anemone – BatmanDuck

以下是更多复杂的生长模拟示例，探索了各种规则和参数：

 

6.0 发展分形曲线

为了创造一些更具象的东西，可以提升这些曲线的维度。记录空间填充曲线的逐步迭代，可以生成一个本质上是“空间填充表面”的东西。这个新表面具有独特的性质：它能够以单一表面的形式填满任意形状和大小的三维空间。当然，它也继承了其源曲线的特性，即其表面积可以不断增加（并且可以无限增加）。

表面展开研究

如果妳在有限的空间中持续（但无限地）以这种方式增加表面积，结果将是一个二维表面无缝地转变为一个三维体积。

 

6.0 龙之足迹

以下是一个将龙形曲线转化为空间填充表面的例子。每一次迭代都会被记录并在深度上偏移，所有这些共同构成了一个表面，使其大致流经这些迭代。这同样是通过 Rhino 和 Grasshopper 实现的。

我认为这种几何形态除了“发展中的龙形曲线”之外并没有正式的名字，所以我将它称为“龙之足迹”。

给模型增加一些厚度后，它就可以被 3D 打印出来。

开发“龙曲线”：龙的脚——3D打印

 

6.2 希尔伯特的帷幕

这里是希尔伯特曲线经历同样的过程，我将它恰当地命名为“希尔伯特的帷幕”。

开发希尔伯特曲线：希尔伯特的帷幕——3D打印

3D 打印空间填充曲线（Henry Segerman 在 Numberphile 的演讲）：

《Developing Fractal Curves》 by Geoffrey Irving & Henry Segerman:

 

6.3 鲸鱼曲线的演变

毫不意外地，这种方法也可以应用于通过微分生长生成的曲线。不同之处在于，这种方法以一种不那么受控的方式填充特定空间。

在这个例子中，Kangaroo 2 被用来将曲线生长为鲸鱼的形状。与之前相同，每次迭代都被用来生成一个单一表面几何体。

差异生长鲸鱼曲线的迭代步骤

开发鲸鱼曲线——3D打印

 

【制作团队】
企划：了有和
脚本：Nick Leung
排版：了有和
校对：Tav、林晨
监制：了有和、Beatrice

版权声明：未经授权，不得转发。

内容版权归原作者所有，内容代表作者观点，我们的服务，和 EasyRef 上的所有内容，均按「现状」提供，不提供任何类型的担保，无论是明示还是暗示皆然，内容及品牌是上传所有者的财产，内容均来源于公开信息。
*已标注信息来源

原文链接：https://wewanttolearn.wordpress.com/2018/01/01/developing-space-filling-fractals/

超薄各向异性网壳

超薄各向异性网壳

Related Posts